

Test Your Knowledge:
Memory Aides
Reading Exercises
Checks & Balances
Reference/Charts, Etc.
- Poker Glossary
- Poker Odds
- Preflop Odds
- Odds for the Flop
- Overcards on Flop
- Odds for the Turn
- Odds for the River
- Overall Percentages
- Hand Simulator
- Pot Odds Calculator
- Probabilities Chart
Poker Rules
- Poker Rules
- Poker Hands
- About Texas Hold'em
- Hold'em Rules
- Omaha Poker
- Limit Poker
- 7 Card Stud
- Variants
Preparation:
- Poker Rules
- Poker Lingo
- Lingo Quiz
- Why Learn Poker?
- Key Poker Skills
- Bankroll
- On to Casino
- Play Money
Poker Fundamentals:
Mental Strategy:
No Limit Hold'em:
Tactical Concepts:
Psychological Concept:
Finding Your Game:
Expert Concepts:
Tournament Poker:
Money Management:
Poker Training- Preflop Odds
Determining Odds Preflop
There are exactly 1,326 different ways you can be dealt 2
card combinations in the standard deck. How do we come up with
this number? Think of it this way, the odds of dealing any card
you name off the top of the deck are one in fifty-two. The odds
of dealing the next card you name are one in fifty-one or 52 x
51= 2,652. These cards can come in either order so divide by two
and you end up with 1,326.
1:326 is a very important number for a hold'em player. This is a
number you're going to have to memorize if your committed to
winning
at hold'em more consistently. By now you can see how a knowledge
of mathematics is crucial. (Note: there are many online
interfacing
odds calculators that offer quick odds statistics however, I
suggest you learn not to rely on them exclusively. Most pros
have learned to memorize
and calculate without them.) Many of the decisions you will have
to make at hold'em involve knowing this number.
Now, there are only six ways to be dealt each pair. You only
have 4 cards of each rank to work with when creating pairs and
there are only six
possible combinations. They are:
1. 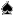 /
/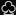 2.
2. 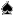 /
/ 3.
3. 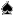 /
/ 4.
4. 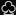 /
/ 5.
5. 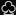 /
/ 6.
6.  /
/
Any two cards that are not a pair can come in sixteen different
ways. Let's look at AK for an example, the A can combine with
each of the four different kings, as can the A
can combine with
each of the four different kings, as can the A , the A
, the A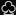 , and the A
, and the A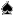 . Four aces
combining with four kings makes sixteen possible combinations.
They are:
. Four aces
combining with four kings makes sixteen possible combinations.
They are:
1. A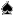 K
K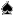 3. A 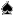 K
K 5. A 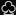 K K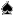 7. A 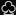 K
K 9. A  K K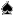 11. A  K
K 13. A  K K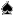 15. A  K
K
|
2. A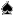 K
K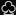 4. A 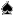 K
K 6. A 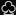 K
K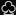 8. A 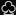 K
K 10. A  K
K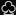 12. A  K
K 14. A  K
K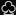 16. A  Kd Kd
|
Four of the combinations above are suited. This is true of
all unpaired hand combinations so, since 16/4=4 we can deduce
that one-fourth of all unpaired two-card hands will be suited.
Now you have learned, without much work, four things:
1. There are 1,326 different hold'em hands
2. There are only six ways to make a pair.
3. There are sixteen ways to make an unpaired hand.
4. One-fourth of those unpaired hands are suited.
5. Additionally, we may deduce that by disregarding suits, there are 169 different possible two-card hands. Any one of the thirteen ranks can combine
with any one of the other thirteen ranks to make a hand (13x13=169).
6. Of the 1,326 total hands, seventy-eight of them are pairs (13 ranks x 6 combinations= 78 different pairs).
7. Since #6 above is true, one out of every seventeen hands will be a pair (1,326/78=17).
8. Since #7 is true, the odds of being dealt any pair you specify (usually aces) are one out of 221.
So if I ask you what the odds of being dealt pocket aces on the next hand, you will say?...220 to 1? Right!
You can also draw this conclusion by dividing the six ways to make pocket aces into the 1,326 possible hands (1,326/6=221).
9. With no information at all about a player's hand, you know that odds are sixteen to six (or eight to three) that he does not hold
a pocket pair. The unpaired hand is two and two-thirds more likely than the pair (6 x 2 2/3=16).






